Implementation Notes on “MACI anonymization using rerandomizable encryption”

Many thanks to Kobi Gurk for the original post introducing rerandomizable encryption to MACI, and to the Dora Factory team for discussions regarding actual implementation details of anonymous MACI.

Adding anonymity to MACI can reduce the reliance on the operator's integrity and further scale decentralized governance and community voting. The original MACI design lacks anonymity between users and the operator. Specifically, a user's behavior is transparent to the operator, meaning that the operator can map the user's behavior to their identity. This contradicts with the notion of anonymization. Ideally, the operator tallies the votes without knowing who voted for what, blocking collusion between the operator and users. To achieve this level of anonymization, MACI needs to hide a user's identity during voting.

A straightforward way is to have users provide zero-knowledge proofs of ownership of valid keys during voting without using or revealing the registered keys, so that the operator doesn't know who's voting. However, for users to provide proofs, the key set has to be public, which allows users to effectively sell keys to others. For this reason, a previously proposed light-weight MACI anonymization was not adopted.

One solution to this problem is to add a 2-of-2 MPC between the operator and a voter, as described in Adding anonymization to MACI. However, implementing 2-of-2 MPC can introduce much overhead and complexity to the system.

A recent post provided one possible solution to MACI anonymization with 2-of-2 MPC using Garbled Circuit and Oblivious Transfer can be found here.

For this reason, achieving MACI anonymization without MPC between users and the operator is preferred. One way to implement a non-MPC anonymous MACI is to use rerandomizable encryption, as described in Kobi Gurk's proposal.

Achieving Anonymization

The key-changing message is decomposed into two messages - a key deactivation message and another message to add a new key .

The message generates a new deactivation record, and the message must provide the deactivation record before adding a new key to replace the previous key. The deactivation record can exist in any form, but it needs to be publicly verifiable.

Anonymization is achieved by the fact that anyone can deactivate their keys at any time, and provide a new key which the operator cannot correspond to any existing key. Thus when a new key is voting, it's anonymous.

The bookkeeping is done through a . The utility of is to keep track of which keys have been successfully deactivated so that both the operator can check it when adding new keys, and the users who want to add new keys can prove ownership of deactivated keys based on it. For this reason, the has to be public.

Each element in contains the key to be deactivated, and its actual deactivation status ( or ) encrypted using the operator's ElGamal key. Note that here the status is then is successfully deactivated, otherwise the deactivation record is invalid.

By encrypting the deactivation status, only the operator can see if the deactivation record is valid or not. Users cannot prove to others they actually deactivated their keys or not.

In addition to deactivation records, a set is used to help the operator to keep track of which deactivated keys have been "used" to generate new keys. If a new key is successfully added, then the operator will add the corresponding deactivated old key to so that the old key cannot be used more than once to activate new keys.

User Proof

To ensure that users do act truthfully, a user has to generate a zero-knowledge proof every time when publishing a new key. They need to prove the existence of their deactivation record without telling the operator which deactivation record is.

Specifically, a user needs to prove the following to the operator:

(1) it owns the private key of the public key to deactivate;
(2) there is a deactivation record in the ;
(3) is rerandomized from .

The user doesn't need to prove the correctness of the status in the deactivation record. Instead, the operator can decrypt the rerandomized version of back to plaintext to confirm the validity of the deactivation record.

The role of ElGamal rerandomizable encryption in MACI anonymization

ElGamal rerandomizable encryption plays an important role to rerandomize the encrypted key status and store them in the , such that (1) the original ciphertext cannot be identified by the operator; and (2) the operator can still decrypt the ciphertext back to key status with the same ElGamal private key.

Since The rerandomizable encryption function converts into as if a new random number is chosen during encryption, the operator can not correspond the new ciphertext to any existing deactivation record from the . At the same time, the rerandomizable encryption function uses the operator's public key for encryption. Therefore, the operator can still decrypt back to the same plaintext. From the user's perspective, the user does not disclose their own deactivation record but discloses the secret information in the deactivation record to the operator, successfully hiding their identity. From the operator's perspective, the operator can verify the validity of the deactivation record.

A Complete Voting Cycle

In an anonymous MACI round, users start with signing up their keys to the operator's registry. All users are encouraged to deactivate their initially registered keys before they start voting.

When the operator receives , it decrypts the message and checks the validity of the key. Then if the key is currently active, it adds a valid deactivation record into with an deactivation status. If anything fails it adds an invalid deactivation record with an deactivation status.

The operator will need to update the withdrawSet periodically. Users have to wait for the latest update before sending the message.

After receiving , the operator decrypts the message and checks the validity of the message:

(1) the proof is valid;
(2) the key status in deactivation record is ;
(3) the nullifier doesn't exist in the set.

If everything passes, a is added.

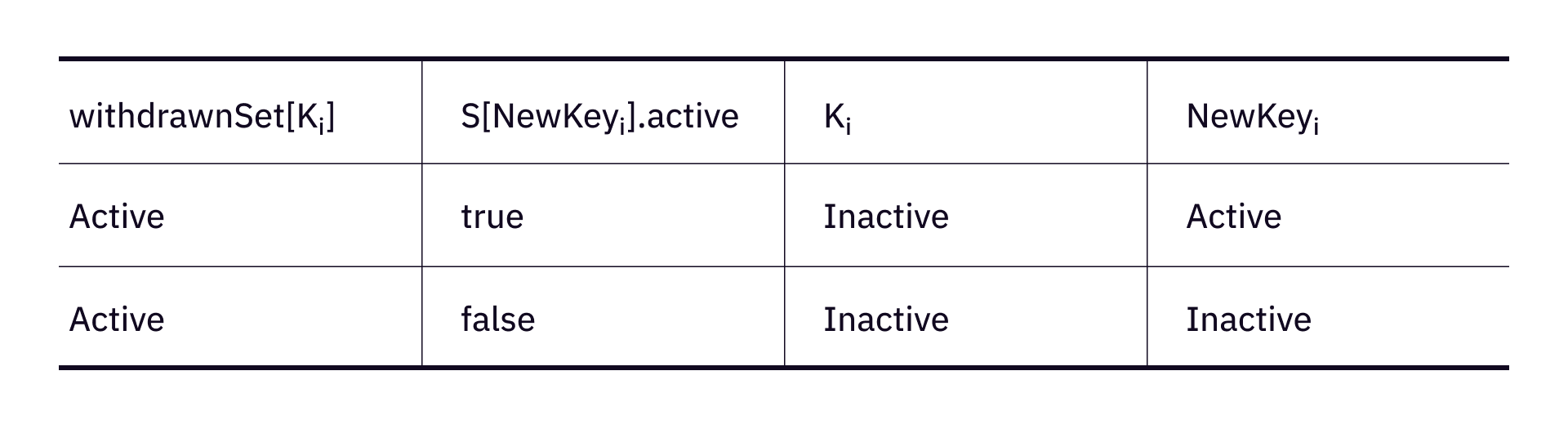
If no user deactivates their keys, the aMACI round will just become a normal MACI round. If too few users deactivate their keys, they might be easily identified by the operator. As a result, the best practice is to have many users deactivate keys at the beginning of a round and update new keys right after the operator updates .