A cryptographic canary against quantum computers

Thanks to Felix Cai for feedback on several engineering challenges of a quantum canary implementation.

Are we cryptographically safe against quantum computers? Transactions carried out on blockchains rely heavily on the security of public-key encryption systems, which means that a signature can be verified easily, but cannot be forged in a computationally feasible way. However, the rise of quantum computers and quantum cryptography algorithms has started to challenge the statement. We foresee that the advance in quantum computing will eventually mark current encryption algorithms insecure.

One way of protecting ourselves against attacks from quantum computers is to build a quantum cryptographic canary, which sends out an alarm if quantum computers of considerable computing power have emerged. This would give us some buffer time in upgrading the encryption algorithms used on blockchains and other pre-quantum cryptographic protocols. We discuss a possible implementation of a quantum canary based on the idea of bounty, and discuss various approaches to incentivise participation.

Bounty Hunting

The vannila version of the quantum canary works like bounty hunting.

To make the bounty publicly verifiable and automated, we can implement it with a smart contract. Specifically, the owner of the smart contract updates a message from time to time, and anyone can access it on-chain. Once a prover comes up with a way of forging the signature of the owner on top of the message, i.e., sign the message using the owner's private key, they can upload it to the canary and receives a small number of tokens.

The canary contract has a variable called safety. Before the appearance of a successful prover, this variable remains true. Once a successful prover manages to forge the signature and uploads it, safety will toggle to false.

The following are some basic variables of the contract set by the owner.

address private immutable owner;
bytes32 messageHash;
uint8 bounty = 1;
bool safety = true;

The following functions can only be called by the owner to adjust the setup of the bounty.

constructor() {
    owner = msg.sender; 
}

function setMessage(string memory _message) public {
    require(msg.sender == owner, "You are not the owner.");
    messageHash = getMessageHash(_message);
}

function setBounty(uint8 _bounty) public {
    require(msg.sender == owner, "You are not the owner.");
    bounty = _bounty;
}

The following functions are accessible by provers. A prover can request to get the hasshed message, and has to return a signed message together with the originally signed message. If the signature is verified, a bounty is rewarded.

function request() public view returns (bytes32) {
    return messageHash;
}

function claim(address payable _prover, bytes memory _signature) public {
    require(recover(messageHash, _signature) == owner, "Verification failed.");
    safety = false;
    _prover.transfer(bounty);
}

Incentivising Participation

Free participation

Generally speaking, anyone who listens to the quantum canary can benefit by simply checking whether the safety variable has toggled. For example, if the current keccak256 signature (256-bit) is broken and the quantum canary catches it, then everyone who uses this algorithm can consider changing the algorithm to alternatives. This is a public good that should be maintained by the public. Therefore, we should encourage messages and signed messages to be uploaded by anyone who has a vested interest, not just the owner.

However, because of the bounty, a cheater may upload many signatures and try to fake the proof. Therefore, participation should not be free. The download fee has to offset the potential free money earned by a cheater. On the other hand, the success of proof needs to be established upon more stringent conditions, for example, a high success rate on a subset of signed messages.

On an important note, to protect the private keys of the participants, we should ask only to upload signed messages using fake private keys, not the actual ones that are currently holding assets on-chain. This is because once the signature of a random message is forged, it probably means that the capacity can equivalently sign any message.

This model is obviously beneficial in the sense that anyone is welcome to participate and participation is easy. However, it becomes impossible to assess the quality of signatures, or the validity of signatures. To encourage participation, uploading should be free, but that reduces the cost of polluting the pool of signatures.

Participation by Invitation

We can invite high-stake users of the protocol (e.g. a public blockchain) to participate only and upload their messages and signatures. This ensures that the signatures are of desired quality, but also rules out free participation. Still, there are centralized risks in an invite only bounty, and it is not completely aligned with the idea of a fully automated canary. Therefore, it might not be the best solution for quantum canaries to be a common practice.

A Betting Game

A betting game is the best way to engage participation, and incentivise participation through monetary reward.

To attract more people into the quantum canary project, we make it a betting game on the outcome of decryption challenges. In each challenge, people are welcome to bet whether a successful prover will emerge within a fixed time limit. In the early rounds of challenges, the signatures are generated by shorter private keys, and are border-line brute-force crackable. Later, challenges get more and more difficult with an increased number of bits in the private key. Bit sizes become realistic. Only quantum computers can break that boundary.

The mechanism works sort of like a sports betting game, with the difference that the one who first wins the challenge can take part of the pot.

Betting stage: both sides can take a bet at a fixed cost. Those who bet that there won't be a successful prover within a fixed time limit will need to upload a message and a signature signed using the required number of bits.
Competing stage: when there are enough participants on both sides, the canary is open. Anyone is welcome to request a subset of "public-key-and-signature pair" samples, and upload their answer in the format of "public-key-and-message pair". If most of the samples have been successfully broken, the prover is considered successful.
Accounting stage: If there is no successful prover in the given time limit, the challenge is not completed. Those who bet so can share the pot. Otherwise, the first successful prover takes the bounty, and the rest is distributed among those who bet the right outcome.

Quantitative Analysis

To find a reasonable setup for our quantum canary, it is important to understand the following question: what should the bounty size be? How long is each challenge? When answering these questions, we motivate ourselves to find a more engaging design of the system.

How much does cracking a private key value?

We talk about values in terms of CPU hours, as it is the only instinsic value associated with anything on the chain.

Bitcoin and Ethereum both employ scep256k1 elliptic curves for public key generation. Neither the generation of a private key, nor verifying if a signed message using a public key is trivial. We want to benchmark our bounty of taking down a 128-bit size private key and a random message to be 1000ETH. This bit-size is of real interest to us, and such a bounty is enticing enough.

To extrapolate the bounty amount, we first ask ourselves how quantum computers actually work. Quantum machines solve factorisation problems in polynomial time. We assume that the relation between the bit size b and the time it takes to decrypt the key is

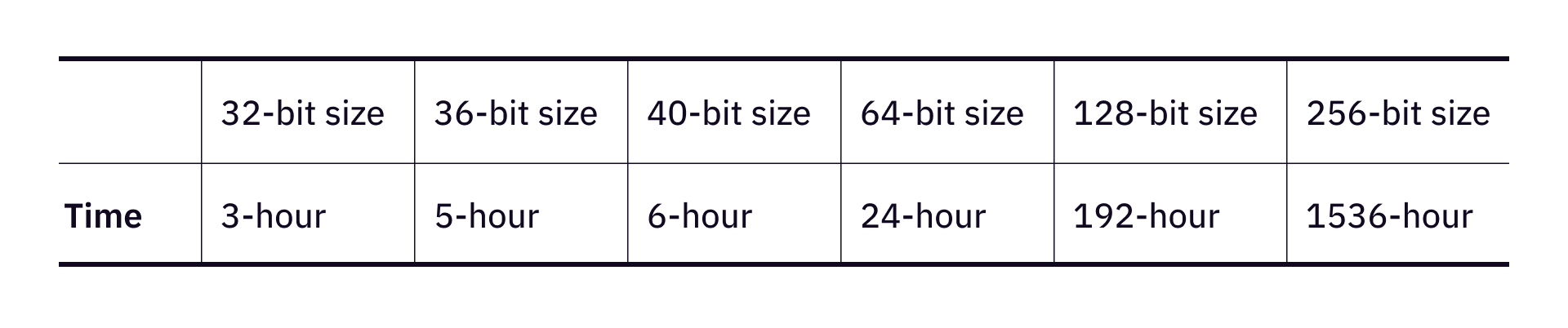
This relationship allows us to come up with the following table of setting bounty sizes.

What do my returns look like?

Since we need a statistically significant result, a large number of signatures is required. Suppose that we need 1000 betters on both sides, then the cost of participation for each side is 0.15% of the bounty. Those who bet on at least one successful prover expect 1:2 return when winning, and those who bet otherwise have a lower return of 3:4 when winning; this is because part of the pot will be taken by the first successful prover (they take 100% of the bounty, which is one third of the money in the pot).

It is tempting to design the canary such that a prover can participate for free. However, consider the following cost analysis and it will become clear why participation fee cannot be zero. A cheater can upload a lot of signatures and keep downloading until the majority of the signatures are those that they uploaded in the first place. Based on the probability analysis in the following section, we see that the cost has to be at least 0.01% of the bounty. Still, this is a very low cost to participate, but not for free.

Can you just get lucky?

We want to avoid the 'win by chance' scenario, by statistically restraining the definition of success. On the other hand, we also want to catch imperfect but effective algorithms.

It is difficult to get the correct number even for the smallest bit-size considered in the quantum canary. So, as long as we ask for more than one private key, we can rule out success by coincidence. However, suppose that a quantum machine is not perfect, which only guesses the correct key half of the time, it is a thread big enough to take into consideration.

What is the likelihood that an imperfect quantum machine completes the challenge? Let us assume that the challenge consists of n public keys, the probability that more than k private keys are successfully generated is

We produce the following table to illustrate different scenarios.

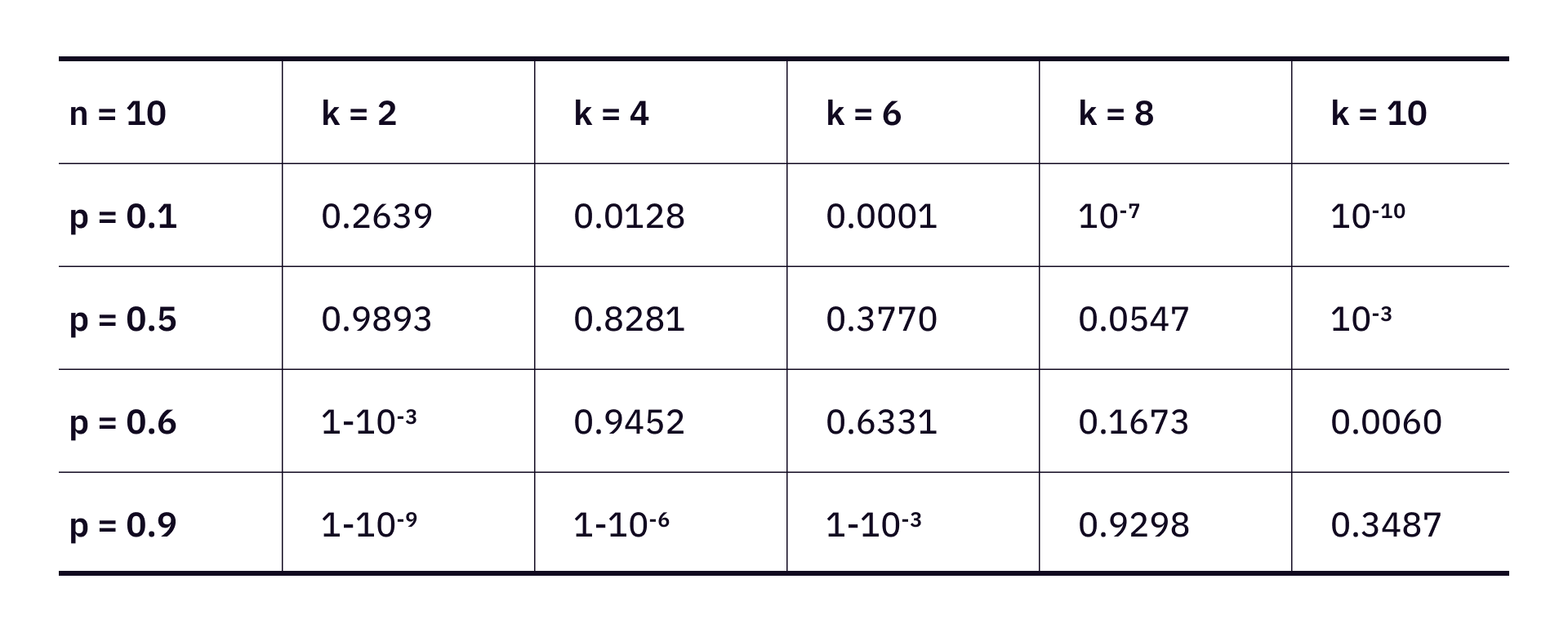
To catch those quantum machines that have a considerable successful guess rate, we probably want to start with 10 public keys, and ask for at least 6 of them to be successfully mapped to their private key.

The speed race

In the previous discussion, we came to the conclusion that the time limit of the challenge should be of the same order of magnitude as brute force search. The estimation is that, for a 32-bit private key, or a string of 8 digits in hexadecimal representation, the time limit can be 3 hours. The time limit on later challenges observes the polynomial growth assumption we established earlier.
As the bit size increases, we imagine that we will be facing a long silence where no quantum computers or computing powers of that strength appear. The quantum canary is quiet, until quantum computers become a reality, and start taking realistic bit size bounties like 64, 128 or even 256.

Conclusion

We see quantum canaries as an effective defense mechanism against attacks from quantum computers. Before quantum computers are fully fledged, traces of its capacity might be detected in the canary.

To encourage participation, we designed a betting game on the safety of encryption algorithms with gradation on the length of private keys. Quantitative analysis is essential in keeping the canary fair and effective. We assume polynomial growth with bit size for quantum algorithms to predict the time it takes to break signatures.

The important note here is that having the project named under 'quantum' does not require the capacity that breaks the current encryption algorithm to be of a quantum nature. In fact, what we are detecting is the existence of computing powers equivalent to that of many-bit quantum computers. We believe that this is a broader question to ask, but also a more meaningful one.