How do hash-based post-quantum digital signatures work? (Part 2)

VegeBun

In the previous article, we introduced several hash-based post-quantum digital signatures. Now we move on to discuss more recent digital signatures, among which SPHINCS+ is included in the third round of NIST recommended signature schemes.

Hash to Obtain Random Subset

Hash to Obtain Random Subset (HORS) is an FTS (few-times signature) signature algorithm. An FTS algorithm can be used to sign messages for a few times, each time it is used, some information is exposed, reducing the key’s security.

HORS divides a hashed message into chunks. If a message is divided into chunks, and each chunk has bits, we have .

As a result, we can generate private keys with a PRG function: . Correspondingly, we can get public keys using a cryptographic hash function: .

Same notation is used across the article to make it easier to read.

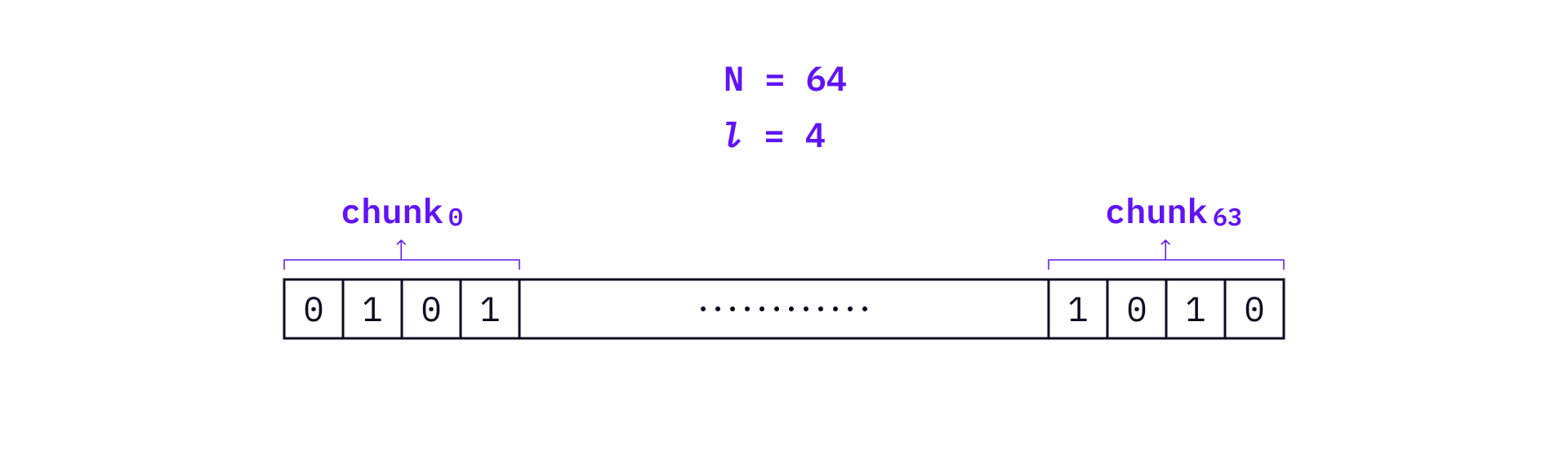
In the above example, a message is splitted into 64 groups and each group has 4 bits. So HORS prepares for private keys . Public keys are computed by applying a cryptographic hash function on each of the private keys.

A HORS signature will be computed as follows:

  1. Compute the decimal values of each message chunk from the message digest. For example, the decimal value of the first chunk is 5.
  2. Compute the signature of the th chunk using its decimal value. In the above example, the signature of the first chunk is .
  3. Generate signature of this message with

To verify the signature, hash the signature chunks one time and check whether the results are consistent with the public keys.

HORS Tree

It’s not difficult to see that HORS public keys are very long. HORS Tree (HORST) was introduced in the SPHINCS paper to reduce HORS public key size with Merkle tree style technique.

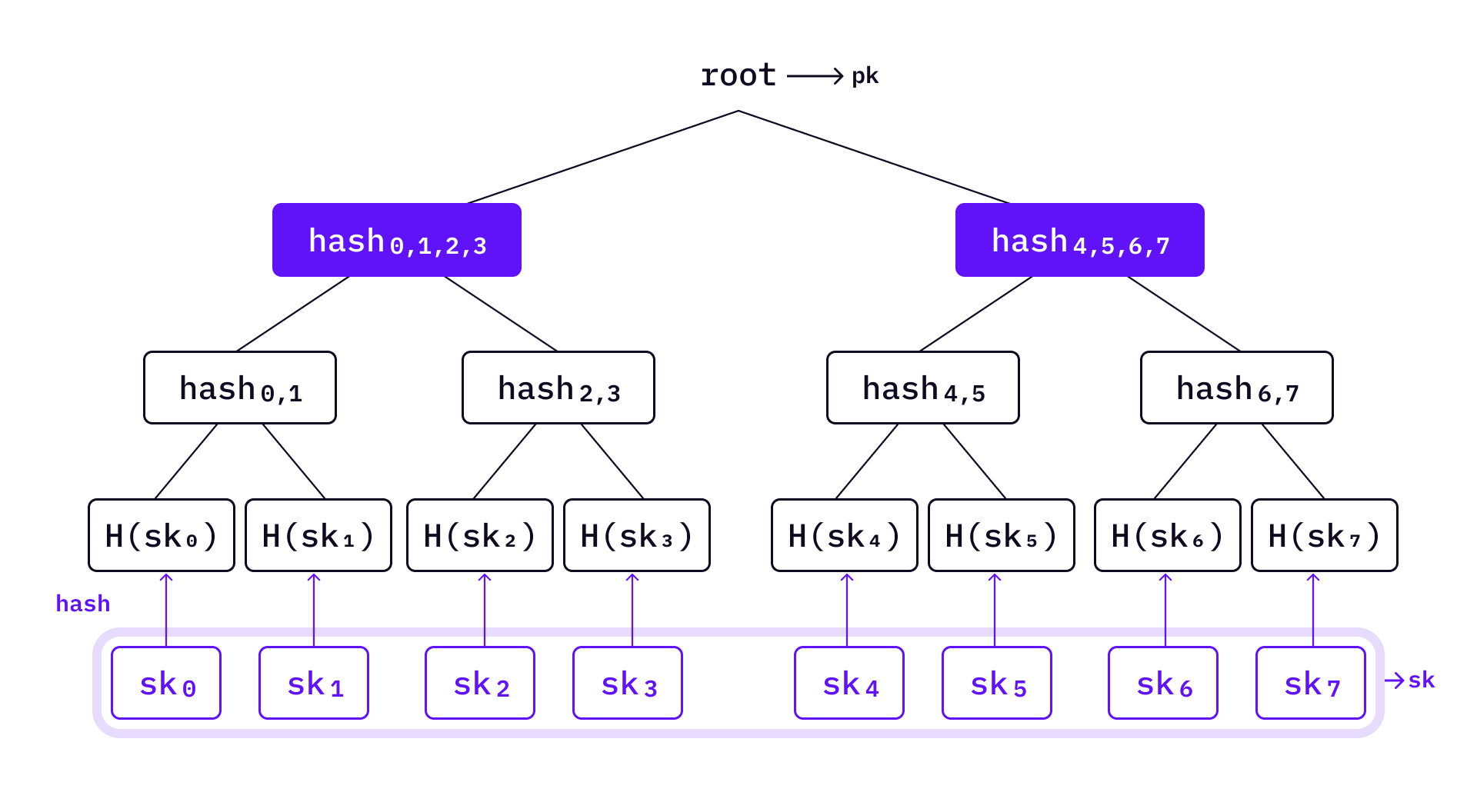
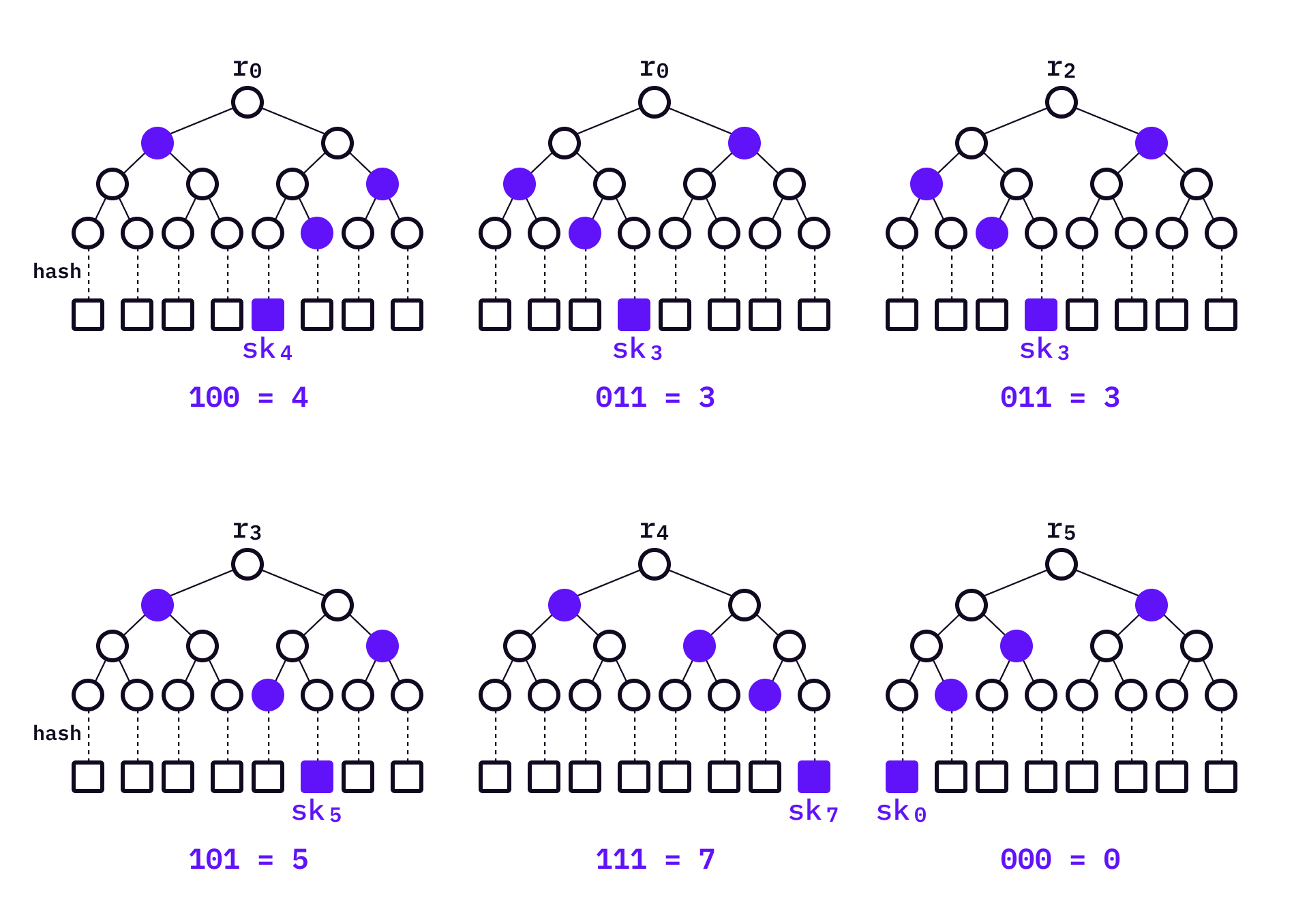
Like HORS, HORST also divides the message into groups. We will use the same example as in HORS — generate private keys with PRG function:. These private keys are used to construct a HORS tree of which the root is the public key and the leaves are private keys. The figure above is an example.

Bitmasks are used in HORST. Before applying the hash function, the two values will XOR with their corresponding bitmasks. Each level of the tree has two diferent bitmask values and , they will XOR with left and right nodes. Therefore, the HORS tree of height will need bitmasks in total.

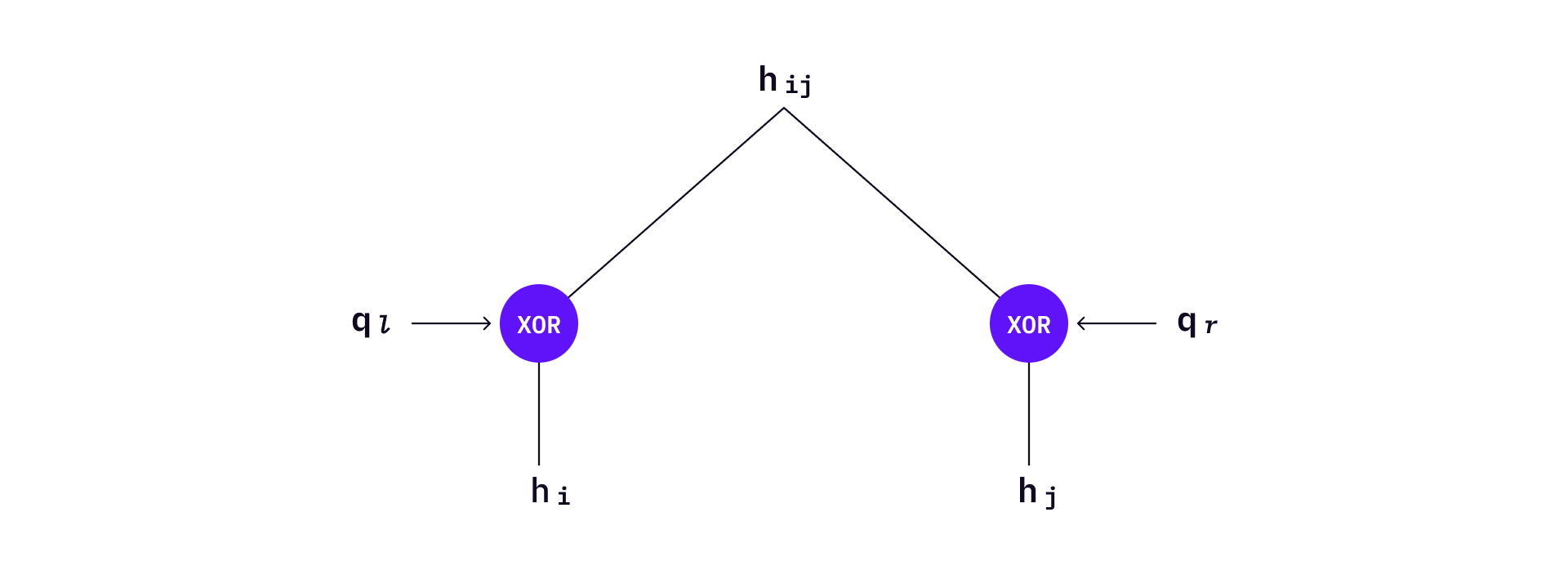
To sign a message, HORST will select the corresponding private key based on the decimal value of each message chunk — same as in HORS. Then an authentication path is generated according to the leaf . For each message group, the signature is . By doing this, the HORS tree root alone can be used as the public key, significantly reducing the public key size.

Intermediate nodes can also serve as authentication roots of HORST. In the example below, and are chosen as two intermediate nodes to authenticate the leaves. You may ask which level should be selected as the authentication root? In HORST, it specifies that the selected level should meet this condition: .

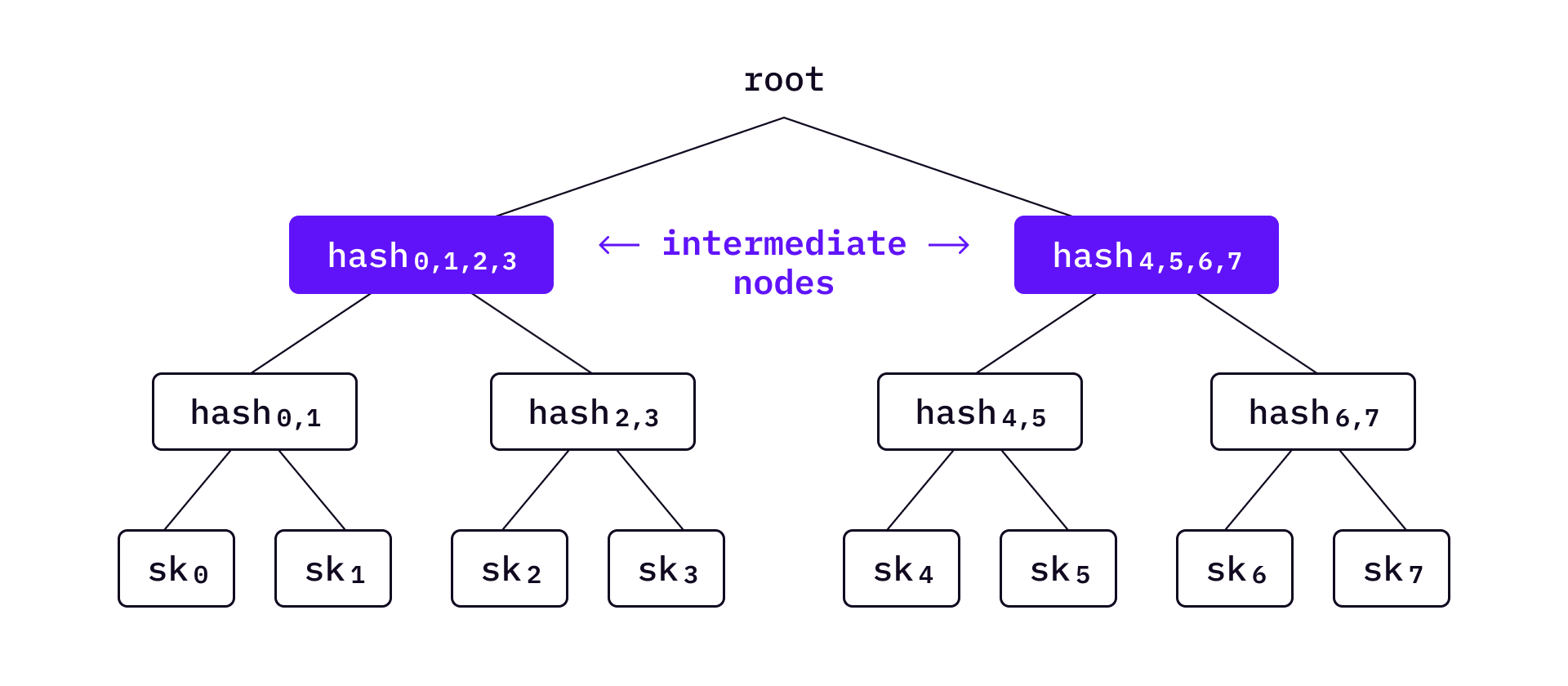
Let’s denote the authentication nodes as . We can generate the signature of HOST: .

The lower on the tree we move , the shorter will be, but the more elements will have — an obvious tradeoff.

Lastly, when verifying a signature, the verifier computes the hash based on and , then compares the value of against values in . The signature is validated if . After all verifications are passed, the verifier can further calculate the root node of HORST. Later in SPHINCS, this root node will have another function and we will further introduce.

SPHINCS

Now based on HORST and WOTS+, a new stateless hash-based signature algorithm called SPHINCS can be constructed.

Note that although previous key management schemes like WOTS+ and HORST can manage large numbers of keys, keys must be pre-generated in order to compute the Merkle root. This limits the number of keys that can be managed. SPHINCS is able to manage a significantly larger number of keys without pre-computing all leaves by leveraging two techniques:

  • Hyper-tree
  • Random key path addressing scheme

A hyper-tree is a tree of trees. Assume the height of the hyper-tree is , which consists of trees of height , and there are levels of L-trees.

This figure shows a specific hyper-tree path after using SPHINCS to sign a message .

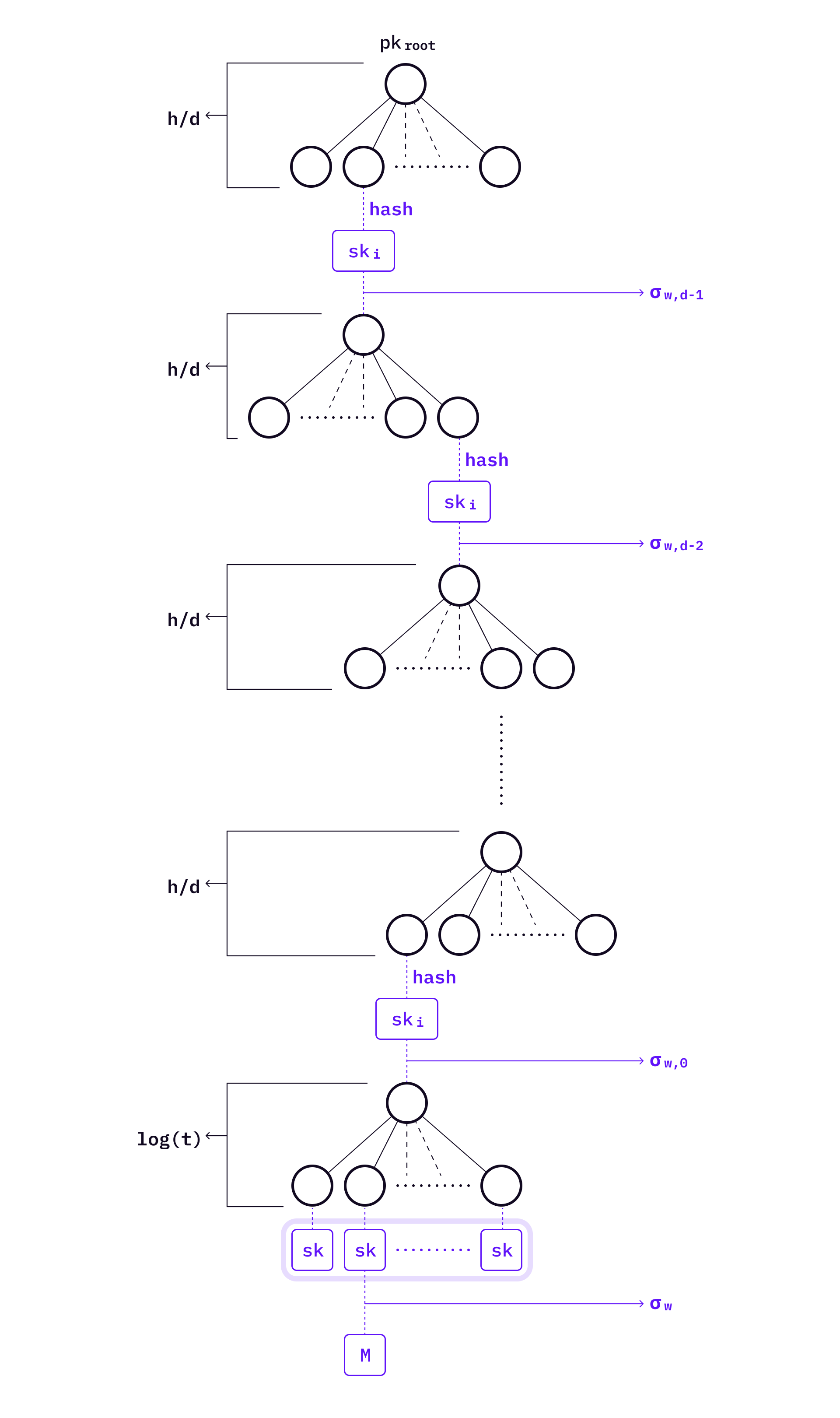
Given such a large structure, one may ask two questions: (1) what are all these trees used for, and (2) what does an authentication path look like across the hyper-tree?

One important thing to know first is that the hyper-tree described by SPHINCS is a conceptual structure — we don’t have to build all the sub-trees on the hyper-tree at once. Trees covering a specific path on the hyper-tree need to be generated only when signing a message.

At the very bottom level of the SPHINCS hyper-tree, there is a level of HORS trees which contain private keys to sign messages. When there is a message, SPHINCS selects a HORST to sign the message, and then generates a signature .

The level above HORST — level — has all L-trees that consist of WOTS+ key pairs. Each leaf of these trees is the public key strings of WOTS+, and their corresponding private keys are used to sign the root of the trees on the next level (from level to level ).

You might have noticed the following features of hyper-tree:

  • There is only one tree on level which is the top tree.
  • There are trees on level , and the root of the tree in level will be signed by the WOTS+ private key of the tree on level .

It means that WOTS+ trees and HORS trees are independent from each other, even though they are selected on the same path to authenticate a signature. This useful feature helps avoid pre-computing all trees during key generation, hence allowing a really big number of keys to be managed under a single SPHINCS public key. The large key space also makes SPHINCS practically stateless signature scheme.

As we mentioned earlier, SPHINCS only identifies specific paths in the hyper-tree when signing a message. You may ask, how is this path generated?

SPHINCS has an addressing scheme to locate the WOTS+ public keys in the hyper-tree. The address format is as follows: which level of hyper-tree, which tree on this level, which leaf from this tree. With this format, we can uniquely determine the WOTS+ public key’s location of each level of the hyper-tree.

Generate SPHINCS private key

When signing a message, first generate SPHINCS private key and public key. The private key consists of three parts:

  • (n-bits) and (n-bits). These two keys are generated by a PRG function. will be used to generate random seeds of HORST and WOTS+ priate keys. will be used to generate an unpredictable index and the hash of the message.
  • bitmasks : Bitmasks are used in several primitives — FORS, HORST, L-tree, hyper-tree. FORS needs bitmasks, HORST needs bitmasks, and L-tree needs bitmasks. The hyper-tree needs bitmasks where .

Generate SPHINCS public key

The SPHINCS public key is the root of hyper-tree, which is a public key of the top level WOTS+ root. The address of the top-level trees’ leaves (level ) can be described as .

First, generate the seed and use the seed to create the private keys of WOTS+. Then compute the WOTS+ public key with in level , it is also the public key of SPHINCS:

We use to denote random seed generation functions across this article.

Sign a message

Now we are ready to create SPHINCS signatures. To sign a message, first create a HORST, and then generate a specific SPHINCS hyper-tree path.

In order to generate the HORST key, first determine the address of the HORST key pair; then generate the corresponding random seed; then create HORST keys through the seed. Lastly use the HORST keys to sign message and generate all WOTS+ signatures in the same way: Address → seed → key pair → signature.

Here comes the details:

  • Generate two random n-bits and by

    • compute the message digest
    • compute HORST address and

  • Generate HORST key pair and HOTST signature

    • generate HORST key pair seed by
    • generate HORST signature and public key by

  • Generate all WOTS+ signatures along the SPHINCS path

    • compute all addresses of WOTS+ in the path where is the level and
    • compute all the seeds
    • generate WOTS+ signature by where is the root of the tree of level. Also we need to generate the authentication path of corresponding WOTS+ public key.

The SPHINCS signature is

Verify signature

The verifier follows the following three steps to verify :

  • check HORST signature:

    • compute message digest
    • verify : , reject if the result doesn’t equal auth path root of HORST.

  • check all WOTS+ signatures:

    • check by ;
    • check the by where
    • reject if any one of the WOTS+ signatures cannot be validated.

  • On hyper-tree level , the verifier gets the root of the hyper-tree. If the , the is validated, otherwise reject.

Although the whole signature scheme looks complicated, the idea is simple: hyper-tree allows a much bigger key space without the need to pre-computing all keys and intermediary nodes.

With an understanding of SPHINCS, we are now introducing the state-of-art hash-based signature scheme — SPHINCS+. But before moving into SPHINCS+, we need to introduce one more primitive.

Forest of Random Subsets

Forest of Random Subsets (FORS) is an improvement of HORST.

Like HORST, it first splits the hashed message into many chunks. The private keys will be hashed and become leaves to construct a tree. The difference is, each tree has its own root. The FORS public key is simply the hash of the roots.

Assume and , the scheme will generate private keys.

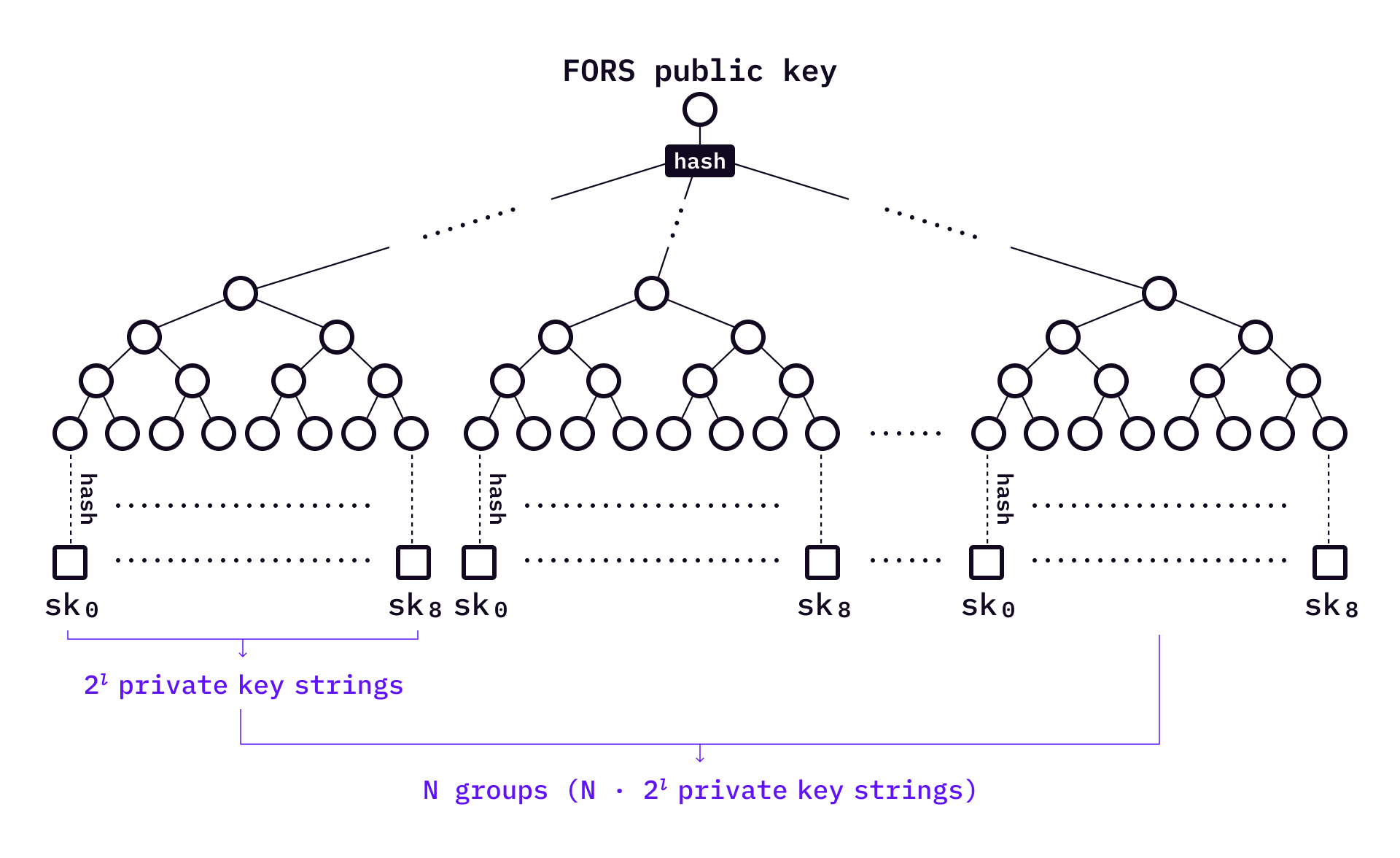
When signing a message, is splitted into 6 groups and each group has 3 bits. For example, if H(m) is 100 011 011 101 111 000, we can choose the corresponding leaf based on decimal values to generate a signature .

In the above example, each private key has a corresponding authentication path. The signature is where the superscript is the tree index, and the subscript is the leaf index within a tree.

To verify a signature，the verifier computes all roots from according to and hashes all roots, if the hash equals the FORS public key, the signature is validated, otherwise reject.

SPHINCS+

Among the latest hash-based signature schemes, SPHINCS+ has great advantages in speed, security and signature size. More specifically, SPHINCS+ is a signature framework rather than a single signature scheme, because there are many parameters which provide flexibility, allowing users to make application-specific trade-offs in terms of signature size, signature speed, required number of signatures, and required security level.

In general, the ideas of SPHINCS+and SPHINCS are quite similar, but there are some differences in details:

  • SPHINCS uses HORST to sign messages, SPHINCS+ uses the FORS to sign messages.
  • Although the selection of leaf nodes by SPHINCS+ is random, it uses a publicly verifiable method.
  • SPHINCS+ introduce a tweakable hash functions to further ensure security.

With an understanding of SPHINCS, we can directly explain the key generation of SPHINCS+ which is similar to SPHINCS.

The public key consists of two n-bit values: the top-level root node from hyper-tree, and a random public seed .

In addition, the private key consists of two more n-bit random seeds: which is used to generate WOTS+ and FORS secret keys, and which is used to generate randomized message digests.

Generate signature

SPHINCS+ signature consists of a FORS signature on a digest of the message, a WOTS+ signature on the corresponding FORS public key, and a series of authentication paths and WOTS+ signatures to authenticate that WOTS+ public key. However, SPHINCS+ differs from the original SPHINCS in how the message digest is computed and how leaves are selected.

  • SPHINCS+ pseudorandomly generates a randomizer based on the message and . can optionally be made non-deterministic by adding additional randomness . This may counteract side-channel attacks that rely on collecting several traces for the same computation. Note that setting this value to all-zero string (or using a low-entropy value) does not negatively affect the pseudoran- domness of . Here which is part of the signature.
  • Using R, we then derive the index of the leaf node that is to be used, as well as the message digest where means message digest and means leaf index. is an additional keyed hash function to compress the message.

In contrast to SPHINCS, this method of selecting the index is publicly verifiable, preventing an attacker from freely selecting a seemingly random index and combining it with a message of their choice. Crucially, this counteracts multi-target attacks on the few-time signature scheme. As the index can now be computed by the verifier, it is no longer included in the signature.

The SPHINCS+ signature is
where is the signature of FORS.

To verify , complete two steps:

  • Check the FORS signature:
    • Generate message digest and leaf index using the same operation as in signing.
    • Check the signature by .
    • To verify the signer’s , verifier can also compute and compare it.
  • Same as SPHINCS, check the WOTS+ signatures of each level in SPHINCS+.

Will hash-based signature schemes be actually useful?

As mentioned in the previous part of this article, there are several hash-based signature schemes that we haven’t included. However, by introducing Lamport, WOTS, XMSS, WOTS+, HORST, SPHINCS, and SPHINCS+, we have outlined the methodology and start-of-art developments of hash-based signature schemes.

It might seem odd for hash-based signature schemes to generate bags of private key strings, but this is a great advantage at the same time — the security assumption of hash-based signature schemes only rely on hash functions.

Other than hash-based signature schemes, there are a few other paradigms to create post-quantum signatures (read this article for more benchmarks). We will cover some important non-hash based quantum-safe signature schemes soon.