One class of post-quantum digital signatures is hash-based digital signature schemes. Unlike the current digital signature schemes used to validate blockchain transactions, hash functions provide much less structures for quantum computers to exploit, and are widely believed to be quantum-safe. The goal of this article is to provide an up-to-date overview of hash-based digital signatures and explain how they work in detail.
Digital signatures widely used on current blockchain infrastructures, such as BLS and ECDSA, are based on the discrete logarithm problem.
For those who are not familiar with digital signatures, there are four parts of a signature scheme: System Generation (SysGen), Key Generation (KeyGen), Signature Generation (Sign), and Signature Verification (Verify).
For example, in ECDSA public key
The BLS signature scheme is constructed on a pairing group
Because quantum algorithms being good at finding periodicity of some functions, it uncovers special structures of classically hard problems like factorization and discrete logarithm. When quantum computers with thousands of logical qubits are available, BLS, ECDSA, and other signature schemes relying on factorization and discrete logarithm problems will not be secure.
For example, finding prime factors of a number
Although current-day quantum computers only have a few hundred noisy physical qubits, quantum computer builders do have intensive roadmaps to achieve large-scale quantum computers. Superconducting quantum computer manufacturers like IBM and Rigetti Computing are moving towards 1000-physical-qubit quantum computers, and use tileable modules to obtain larger number of logical qubits. Beyond that, there are several other methods that could lead to meaningful quantum computing systems in the foreseeable future, including Ion Trap, Neutral Atoms, and Measurement Based Quantum Computing.
On the other hand, there is so far no efficient quantum algorithm found to break a hash function, and quantum computers only speeds up birthday attack to
Now let’s look at how hash functions are used to construct digital signatures and go through hash-based quantum-safe signatures.
One-Time Signature Schemes
The first hash-based signature was Lamport Signature first introduced in 1979. It is a one-time signature scheme (OTS) because one Lamport signature key can only securely sign one message. The signature scheme works as follows:
For each message, the signer needs to prepare for two sets of key pairs.
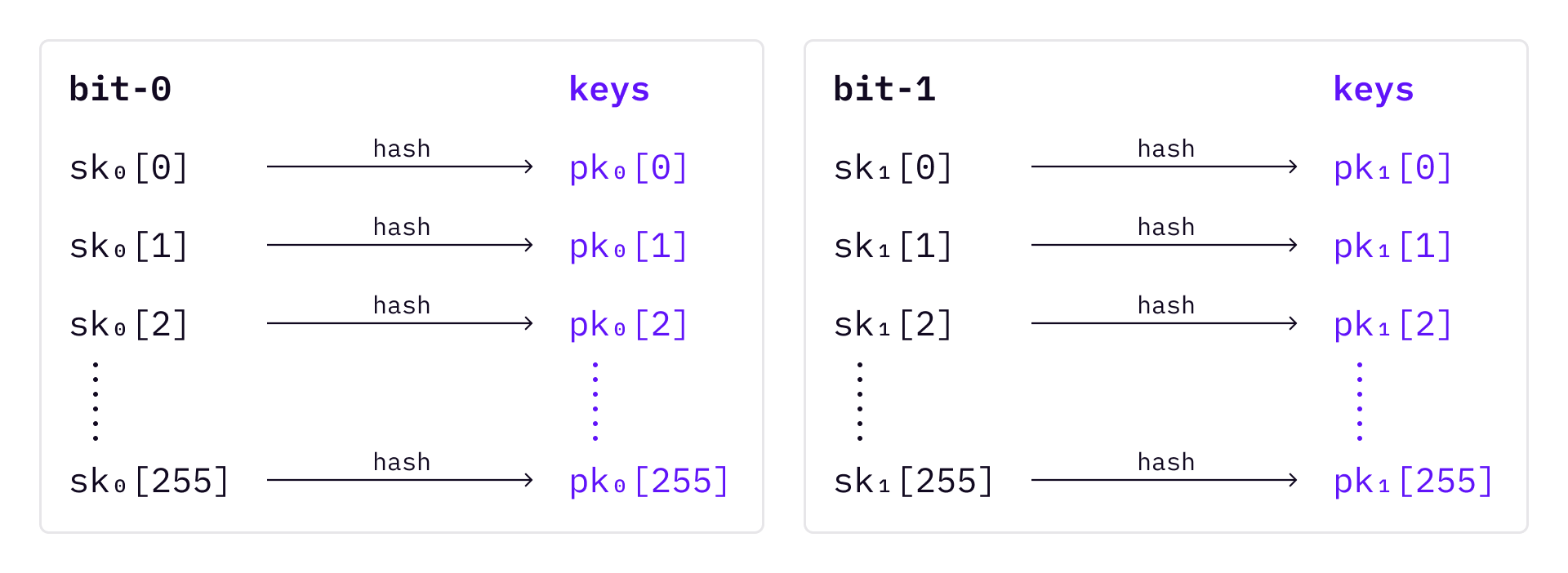
To sign a message, first hash the message into a 256-bit random number; Then, based on the bit value of the hashed number, choose SK accordingly.
Note that we will always sign a digest of a message
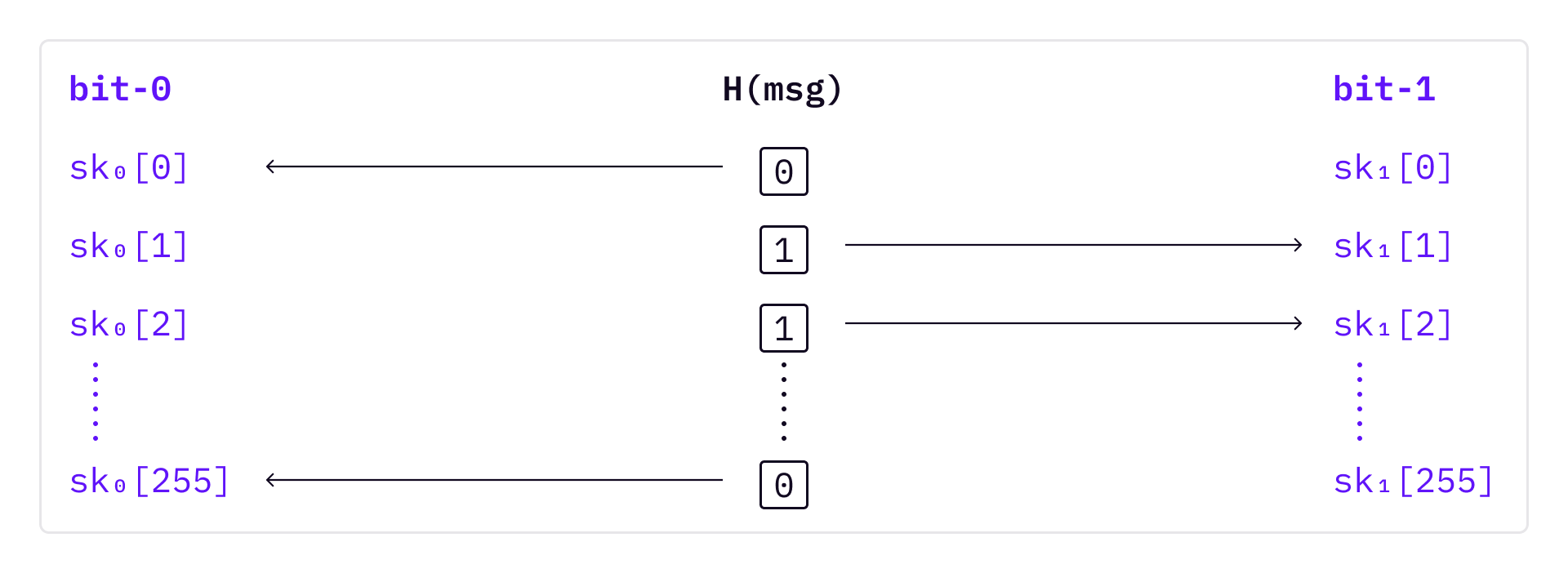
To verify the signature, first compute
The process exposes half of the secret keys after signing any message. So key pairs can only be used once, otherwise an attacker will be able to use the exposed secret keys to validate messages.
Manage OTS Keys with Merkle Trees
From a 21th century crypto user’s standpoint, the Lamport signature scheme might at first look strange and messy. Writing down private key or mnemonic phrase once can be already stressful and annoying, isn’t it driving people crazy if that key can only sign one message, and a different public key has to be shared for every message?
It turns out that the OTS (introduced later) signature schemes can be not that bad, if we can properly introduce mechanisms and tools to manage the keys.
Because Lamport OTS and Winternitz OTS can only sign one message at a time, if multiple messages need to be signed, there must be many keys. The Merkle Tree Signature Scheme (commonly called “MSS”) was invented by Ralph Merkle to manage Lamport OTS keys.
The basic idea is to use Merkle tree leaves to store Lamport OTS keys. Because Merkle tress are binary trees, a Merkle tree of height
When signing a message, one Lamport key pair needs to be picked up from the tree that has not been used before. The signature consists of the index of the leaf, the Lamport public key, the digest of the Lamport public key (the leaf), and the authentication path of that leaf.
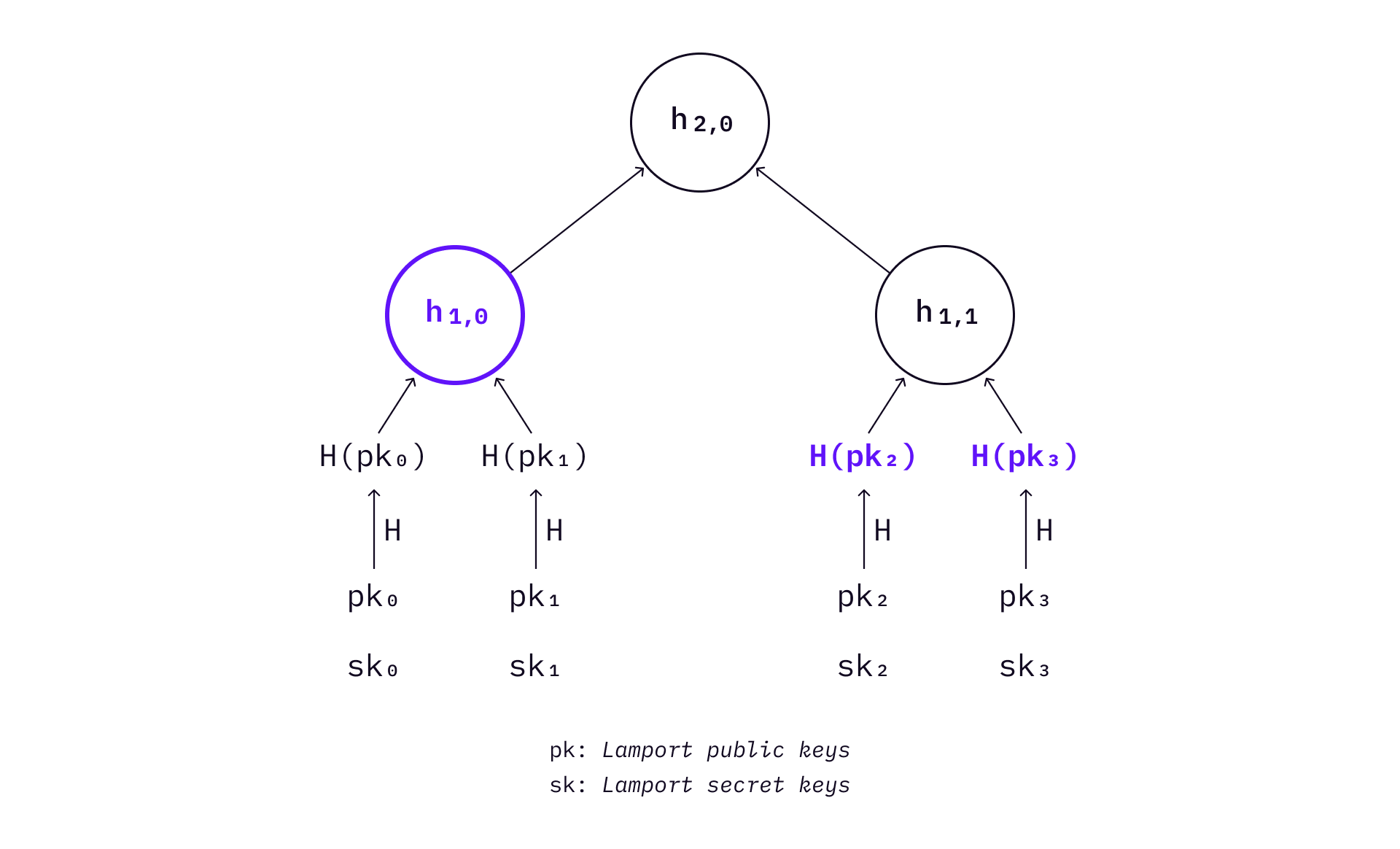
If many messages need to be signed, the above process can be repeated. As a Lamport key pair is a one-time key pair, no leaf can be selected more than once. Therefore, MSS is a stateful signature scheme.
You might also have noticed that the Lamport signature scheme itself does not prevent middle-man attack, if the verifier is given a Lamport signature only.
In order to verify the signer’s Lamport public keys are authentic without Merkle tree, the verifier needs to keep a copy of the keys. Because all the individual key pairs are one-time use only, the verifier then needs to keep a copy of all public keys. Using a Merkle tree effectively allows the verifier to only save the Merkle root instead of saving
As a result of using Merkle tree, signature must include auth path each time - a bit more space, and the verifier computes
Winternitz OTS
Another problem with Lamport OTS is that the Lamport public keys and Lamport signatures are too long. Robert Winternitz provided an improved signature scheme (now called WOTS) that significantly reduced the size of signature.
Instead of preparing private and public key pairs for every bit of a message, Winternitz OTS divides a hashed message
Suppose that we still use a 256-bit hash function on the message, and get a 256-bit digest of the message. In this case,
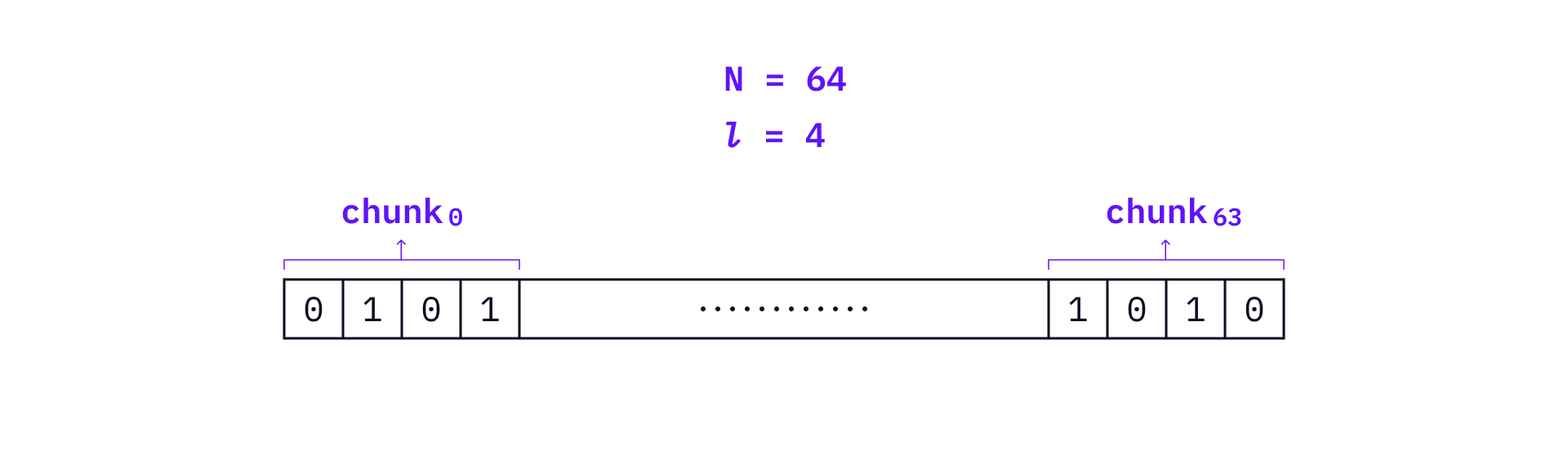
Use the above example,
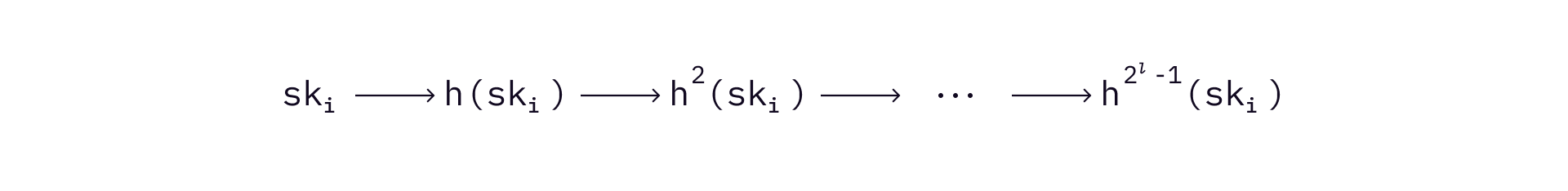
A WOTS signature is generated as follows.
- Compute the decimal values of each chunk from the message digest. For example, the decimal value of the first chunk is 5.
- Compute signature of
th chunk by hashing the corresponding private key times.In the above example, will be hashed times. - Apply (1) and (2) on
chunks and produce signature .

To verify the signature, a verifier will first hash the message and get a 256-bit digest
The verifier then hashes each value the signature
The tradeoff of WOTS is to add more computation in signature generation and verification. As a result, WOTS signatures will be significantly smaller than Lamport signatures (by a factor of about 4 to 8 according to Merkle).
Notably, WOTS is still a one-time signature scheme, because once a key pair is used, an attacker can produce a valid message for each chunk as long as the decimal value of a chunk is smaller than the original value. Therefore, it is not going to be secure at all to use WOTS more than once.
WOTS+
WOTS+ adds randomization to WOTS. It first adds an additional public key
where
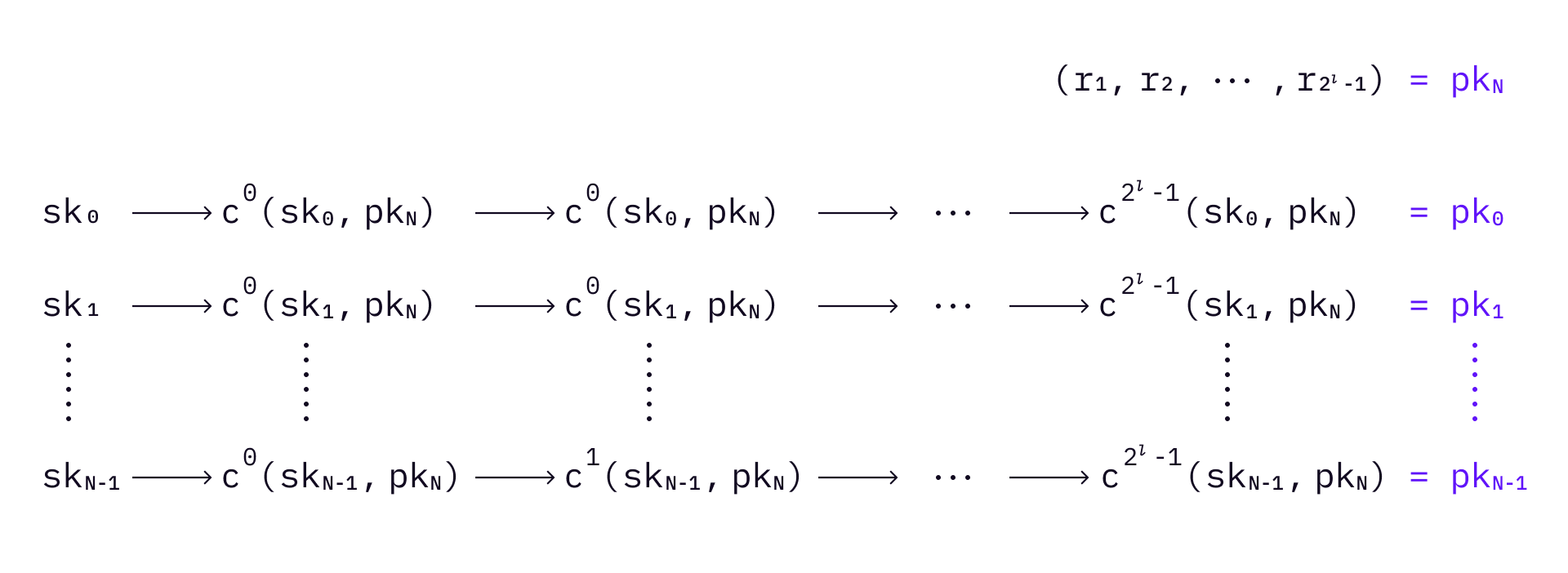
The WOTS+ signature is generated in a similar way to WOTS, with some modifications. It first divides a message
Compute the signature:
Send the signature together with the random number
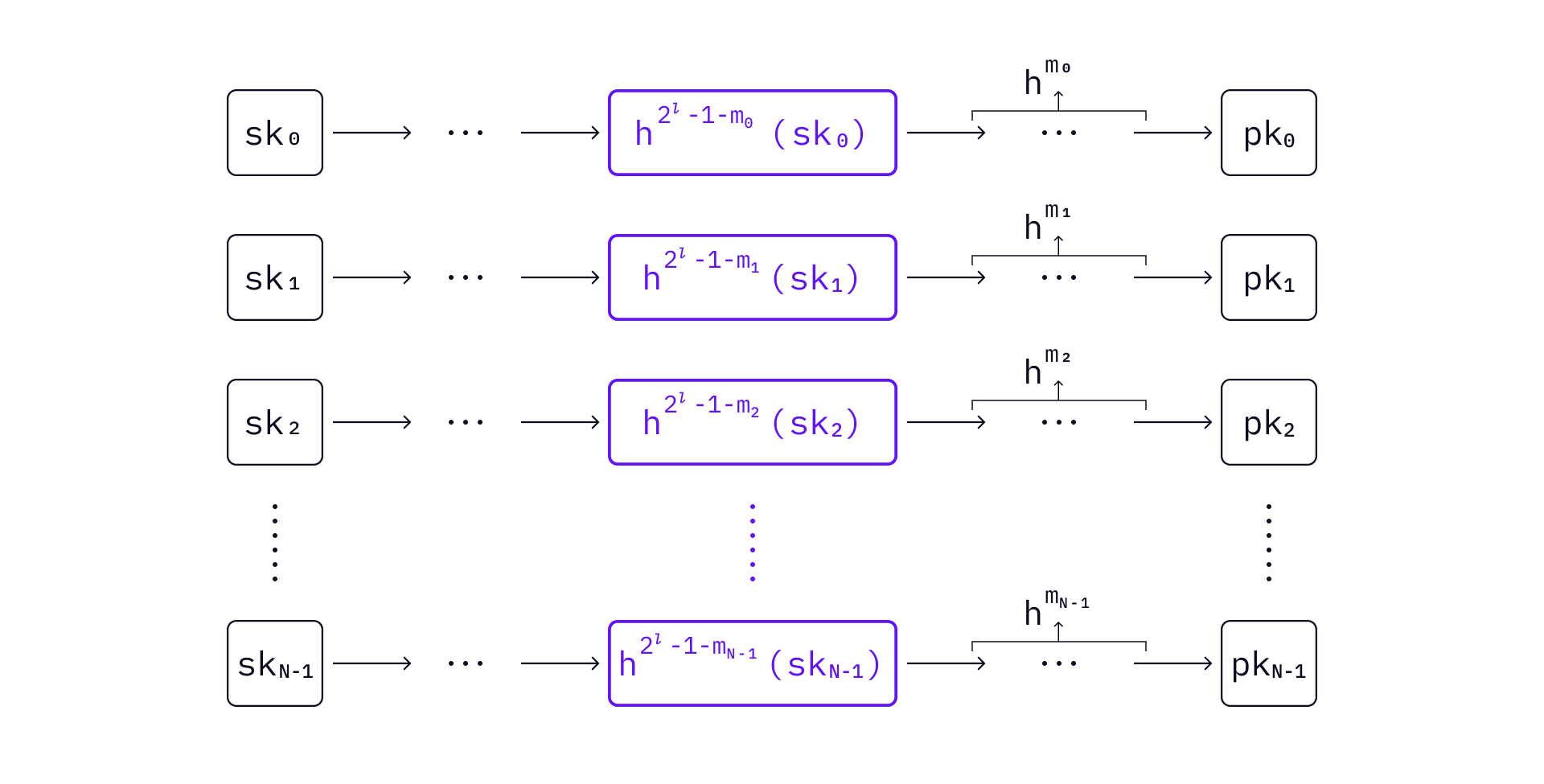
A signature can be verified by continuing hashing the elements from the received
Specifically, compute
If
Although WOTS and some variants of WOTS use simple hash chains, their iteration methods are common and simple. However, WOTS+ has some special mode of iteration, which enables the tight security proof without requiring the used hash function family to be collision resistant.
The eXtended Merkle Tree Signature Scheme
Because WOTS+ is still a one-time signature scheme, key management is important if there are multiple messages to sign.
The Extended Merkle Tree Signature Scheme (commonly called XMSS) uses Merkle tree to manage WOTS+ keys in a similar way that MSS uses a Merkle tree to manage Lamport keys.
Because we already know how MSS works with Lamport key pairs, let's look at the top-level Merkle tree first.
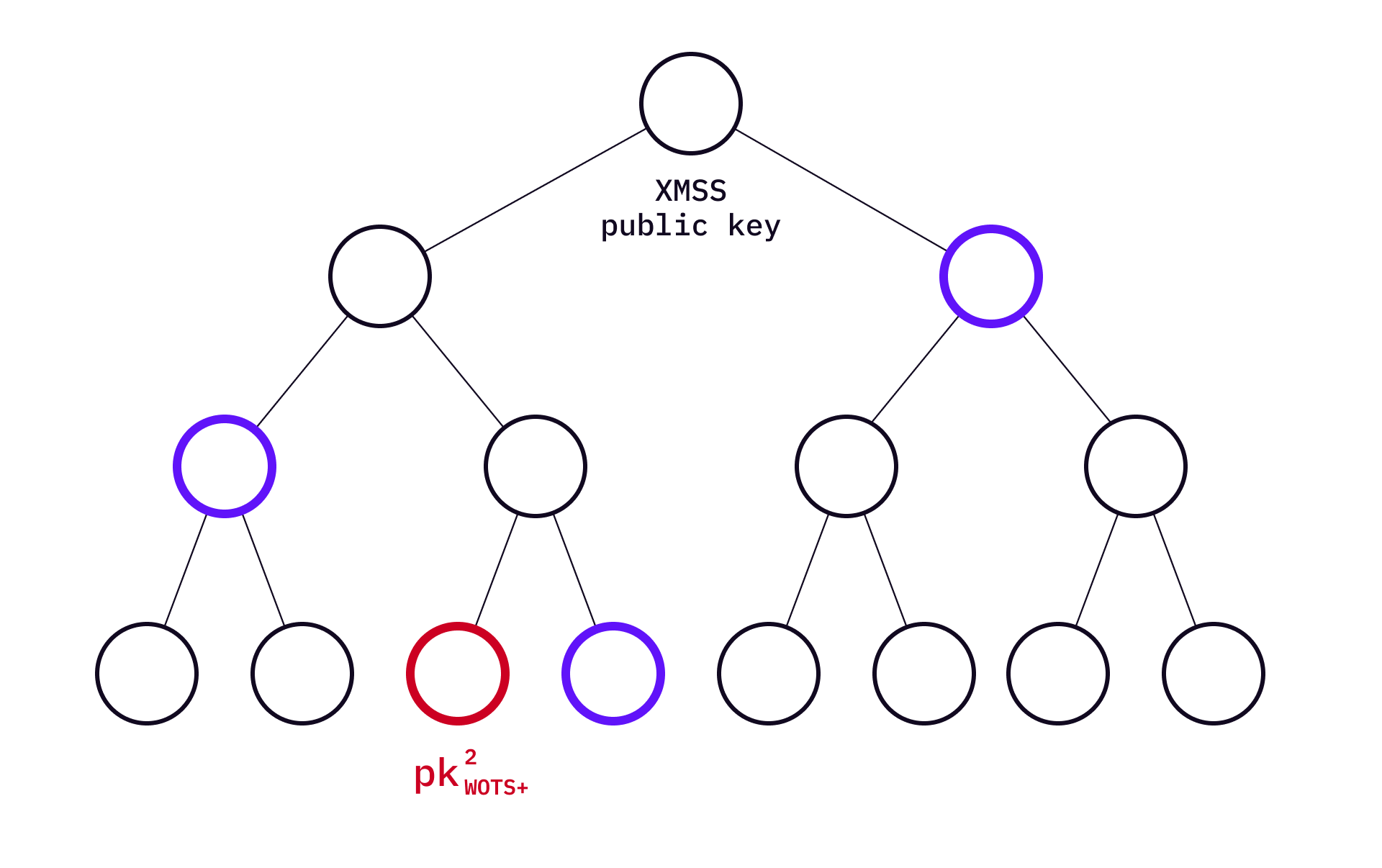
In XMSS, the public key is the XMSS Merkle root. Every leaf of the Merkle tree is a Merkle root of a WOTS+ public key set. To illustrate this, "expand"
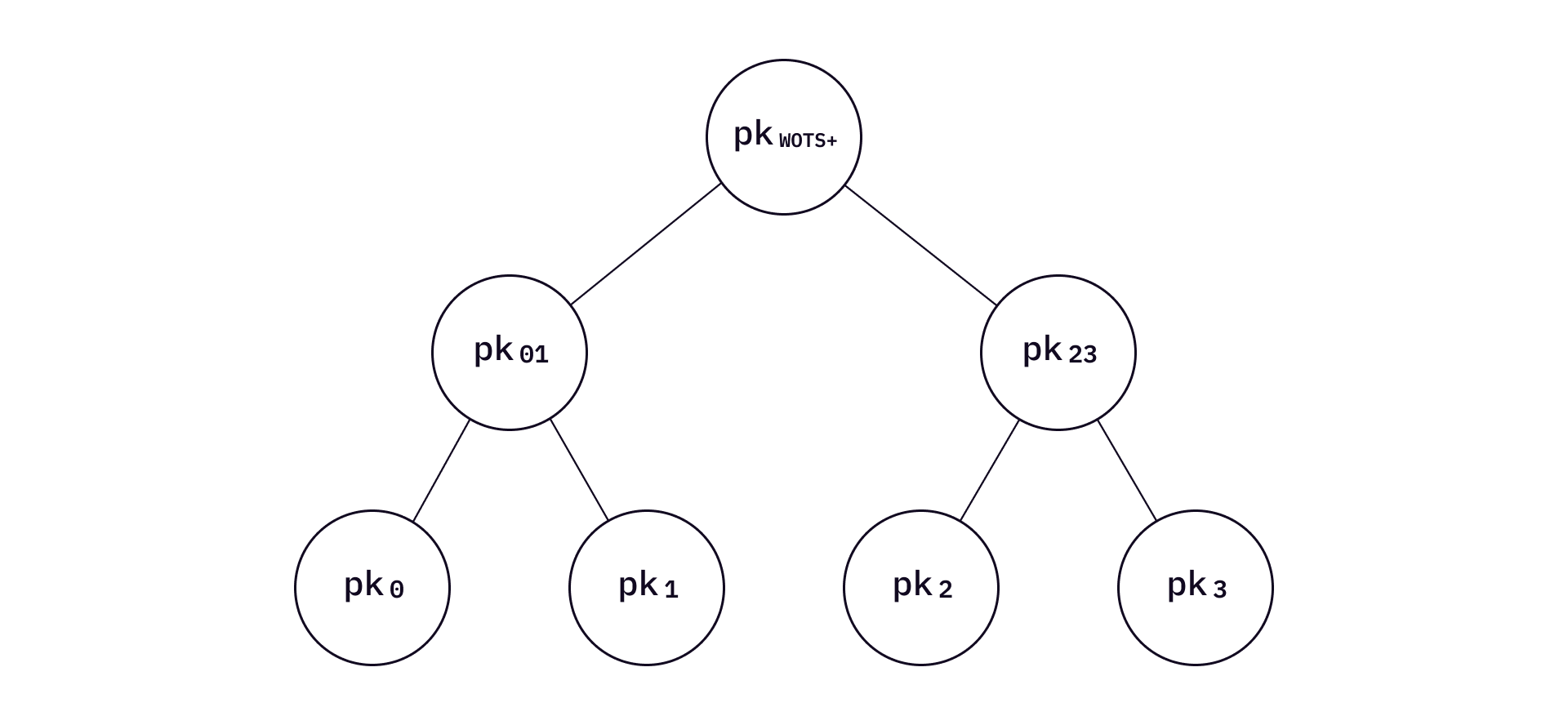
Bitmasks are used in L-trees. Before applying the hash function to two nodes each time, two bottom values will XOR with their corresponding bitmasks. Each level of the L-tree has two bitmask values

Now moving down the L-tree - the leaves of a L-tree are WOTS+ public keys. Every leaf represents one WOTS+ public key, which is created using a chain of hash values from a private key as described in WOTS+.
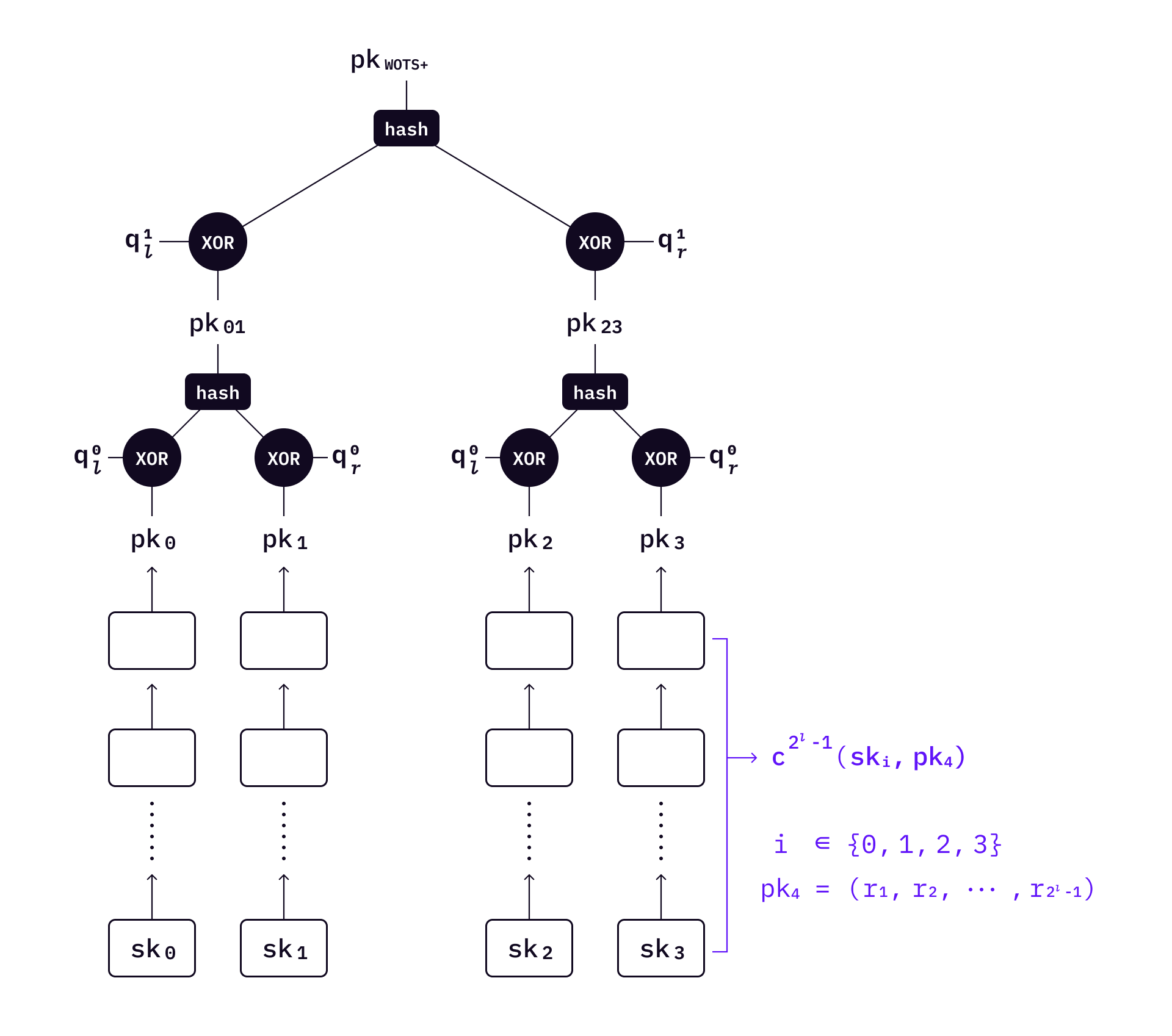
To sign a message
To verify the signature, first verify the
With XMSS, multiple WOTS+ keys can be managed and validated.
Further Reading
The signature schemes introduced in this article are basic building blocks of hash-based signature schemes. More in-depth analysis of algorithmic properties of hash-based signature schemes can be found in this paper by Andreas Hülsing et al.
There are other previously NIST recommended signature schemes (e.g. the Leighton-Micali Signature) and multi-tree variance such as Hierarchical Signature System (HSS) and the multi-tree XMSS (XMSS-MT). These signature schemes and the ones introduced in the first part of this article are not currently recommended by the NIST's recent Third Round of Post-Quantum Cryptography Standardization Process. However, it is important to understand the details of these signature schemes, because newer, and often more complicated signature schemes are designed based on the ideas of these algorithms.
The second part of this article will introduce more recent developments of hash-based signature schemes, including SPHINCS/SPHINCS+, as well as the status of engineering and open source libraries.