Quadratic funding has been widely adopted by many ecosystems — Ethereum, Filecoin, BSC, Solana, HECO, Flow, etc. So far, it has been proven to be effective to fund open source developer projects and public goods in general.
Quadratic funding is allowing people to vote by donation while reducing the impact of whales. In the recent DoraHacks Austin Web3 Hackathon, quadratic funding is doing very well to limit the influence of one-time large donations.
So far, major quadratic funding grant platforms (such as HackerLink, Gitcoin, clr.fund) use the algorithm described in Vitalik Buterin’s paper “Quadratic Payments”.
The paper discussed the quadratic funding process and outlined a few problems, including sybil attack, collusion, and voter incentives. At this moment, quadratic funding platforms have been trying to solve the sybil and collusion problems. HackerLink is integrating DoraID, a proof of identity protocol from Dora Factory (a DAO-as-a-Service infrastructure), providing staking based identity services. Gitcoin just released its GTC token and anti-sybil staking mechanism. clr.fund implemented MACI. All the practices are promising, leading quadratic voting and funding to scale.
However, there is another problem that is rarely mentioned by articles and platforms — the inequality of matching fund distribution.
Quadratic funding amplifies the inequality problem. Projects with a majority number of votes will get an even larger percentage of the matching pool. Most of the time, this is not only creating inequality among early-stage projects when distributing funds, but also discouraging participation (and potentially encouraging sybil attacks even more, e.g. Gitcoin GR9).
In the recent HECO grant on HackerLink, the top project obtained a huge amount of votes (>70% of total votes committed to the whole round), and matched 95% of the total pool of matching fund. After some investigation (data analysis), it was suppressing that most of the contribution was not from sybil attacks, rather, the project mobilized community to vote for them.
(Note: the project did indicate airdrop and other benefits when they mobilized the community, which we do not encourage at this moment. The airdrop / collusion problem is an important topic that we would like to discuss in future articles. Vitalik Buterin has many in-depth articles discussing collusion. In this article, the collusion problem is not addressed.)
After the project dominated the leaderboard with an absolute advantage, the HECO grant received very few submissions for almost two weeks. The project team finally made an announcement to give away up to 50% of their matching pool distribution so that every other project can have a share from the round, and after that we saw an increase of submissions. The HECO grant team finally decided to evenly redistribute the support_area to all projects that have received votes >=10. This is a one-off solution to the problem, but it inspired us to further solve the inequality problem.
The most straightforward mechanism is to use a progressive taxation system.
Progressive taxation was a major invention prior to the WWI. It was widely adopted during the post-war period of the twentieth century, and it has been one of the most important mechanisms to reduce inequality in many countries. As Thomas Piketty pointed out in his book, progressive taxation “offered a way of limiting the inequalities produced by industrial capitalism while maintaining respect for private property and the forces of competition”.
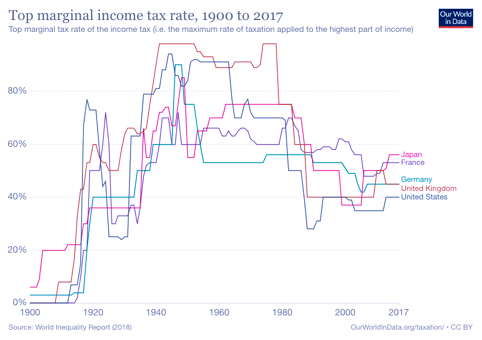
There are multipole ways to implement a progressive tax system in a quadratic funding round. The easiest way, of course, is to design a static progressive tax ladder. After each round, every project is charged with certain amount of tax and later put into a public funding pool. Then the public funding pool can be distributed according to rules that a community think fair.
Here we describe an algorithm that redistributes wealth in each vote() function call.
When a project gains a vote, we define a support area tax ratio k as:
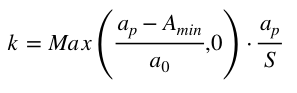
Where,

Based on the formula, a project will be heavily taxed when the following criteria is met:
- The project is ranked on the top
- The project has a dominating percentage of total support area
In this case, the support area will be taxed, and monopoly can be prevented.
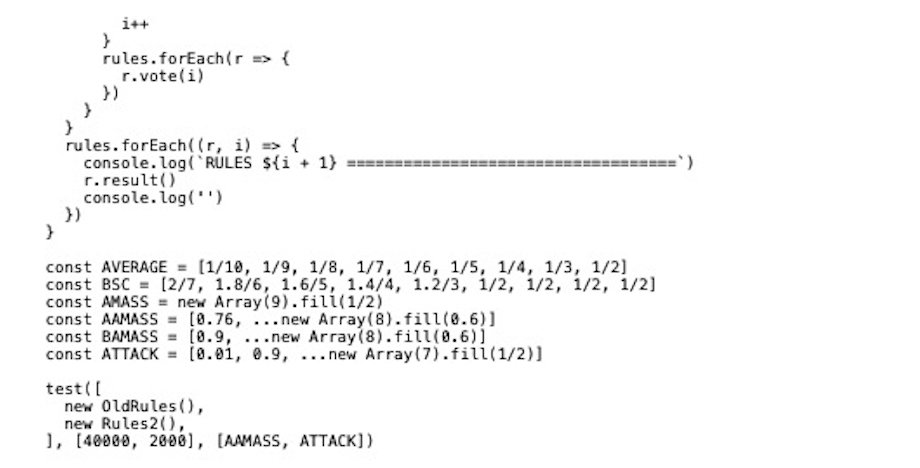
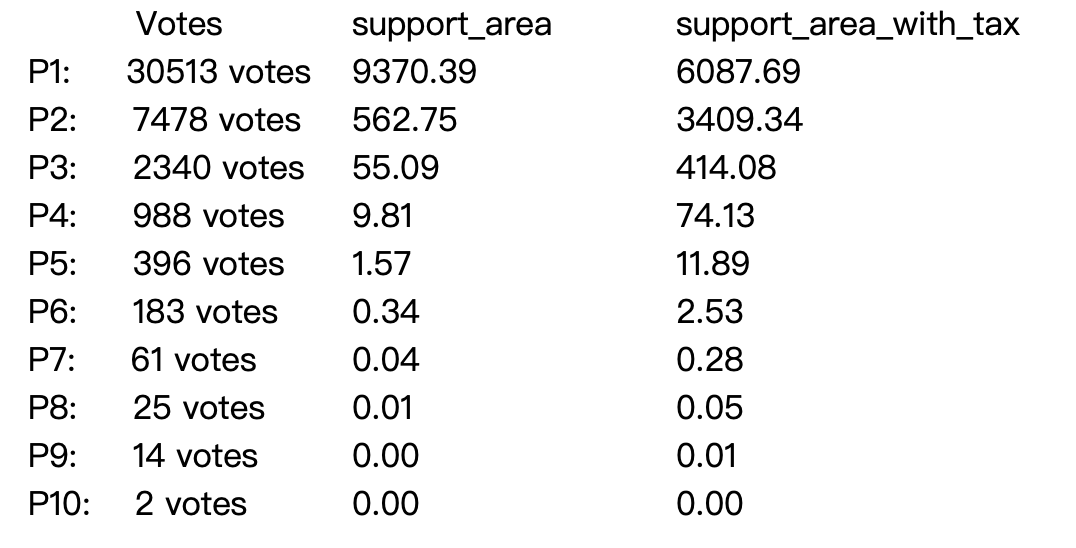
We can simulate a quadratic funding grant with progressive taxation. The result from round with progressive taxation is flattened.
JavaScript code for simulation: